Comparing moment of inertia of bilar pendulum with its theoretical prediction
Description
This experiment is performed to determine the moment of inertia of a bi lar pendulum experimentally and then comparing it to the theoretical prediction. The investigation of the bi lar pendulum includes determining the accuracy of the moment of inertia inferred from the experiment and understanding the underlying experimental process.
Overview
- Physics of a complex pendulum.
- Investigate Newton’s second law for angular motion.
- Determine the moment of inertia for a bifilar pendulum.
- Mathematical manipulation with components of forces.
- Calculating uncertainty and graphical representation of data.
How does it work?
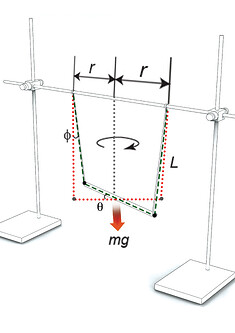
A bifilar pendulum is a straight rod, hanging horizontally from two parallel wires, called “filars”, which allow the rod to rotate freely about the vertical axis.
In the stationary condition, the filars stay vertically and there are no forces in other directions. As soon as the pendulum is twisted, the rods move along with it and the horizontal components of the tension in the filars create a torque, forcing the rod to accelerate back towards the starting position. This torque is proportional to the angle of twist and, just like a simple pendulum, causes the rod to start oscillating about the vertical axis. Moment of inertia plays the same role as inertial in the simple pendulum.
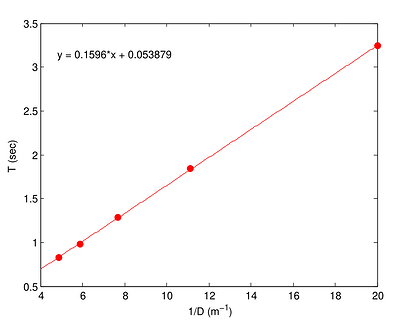
Using Newton’s second law of motion for angular motion, a relationship between torque, the moment of inertia, and angular acceleration is found. This can further be used to find the period of a bifilar pendulum which is also measured using the setup. The model is further used to investigate the uncertainties in the measurement which is a crucial part of the investigation. A graph showing the relationship between the time period and inverse of D (distance between the two filars) is displayed.
Parts Included
- Clamps
- Lab stands
- Pendulum rod
- Filar wires
- Stopwatch
You can get the PDF version of the brochure by clicking on this link.