Exploring the notion of non-linear and chaotic dynamics using magnetic pendulum
Overview
- Exploring the notion of nonlinear and chaotic dynamics using a “magnetic pendulum”
- Experimental observation of the onset of period-doubling bifurcations
- Acquiring time orbits and phase-space diagrams, through simulation and experiment
- Understanding phase portraits
How does it work?
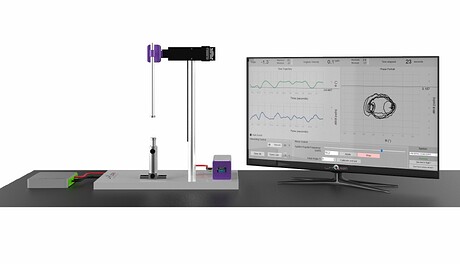
The apparatus, which Qosain Scientific calls Physmag, comprises a pendulum with adjustable height and detachable permanent disk magnets, one set on the tip of the pendulum and the second set on the top of the magnet holder, underneath the pendulum. The shaft of the pendulum is attached to a crank mechanism that gives rise to controlled horizontal oscillation. Our flagship data logger, Physlogger controls the stepper motor that drives the rank mechanism and also logs angular displacement of the pendulum from the optical angle sensor attached with the hinge of the pendulum. Hence we can measure three quantities in real-time:
- Rotation rate of the crankshaft powered by a motor with user-variable RPM
- Angular displacement of the pendulum measured by our specialized analog angle sensor
- Derivative of the angular displacement is computed in our software
What does the Physmag show?
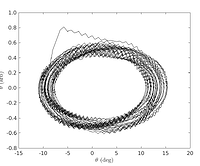
This apparatus can be used to study nonlinearities appearing in the trajectory of the oscillating pendulum. For such a nonlinear pendulum, the simple idea that the time period does not depend on the oscillation amplitude breaks down. Users of Physmag can readily study this in the following graph.
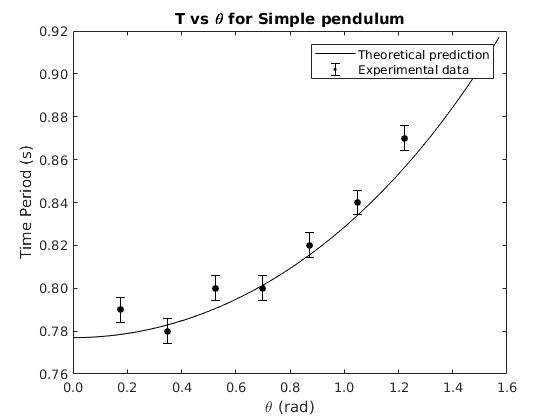
The time period is analytically shown to be,
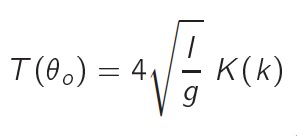
where the elliptic integral is given by,
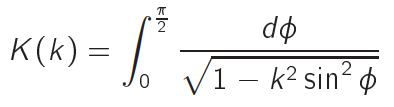
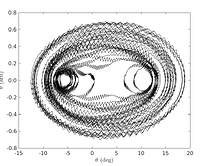
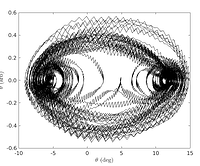
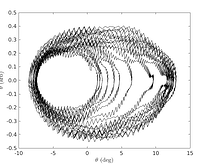
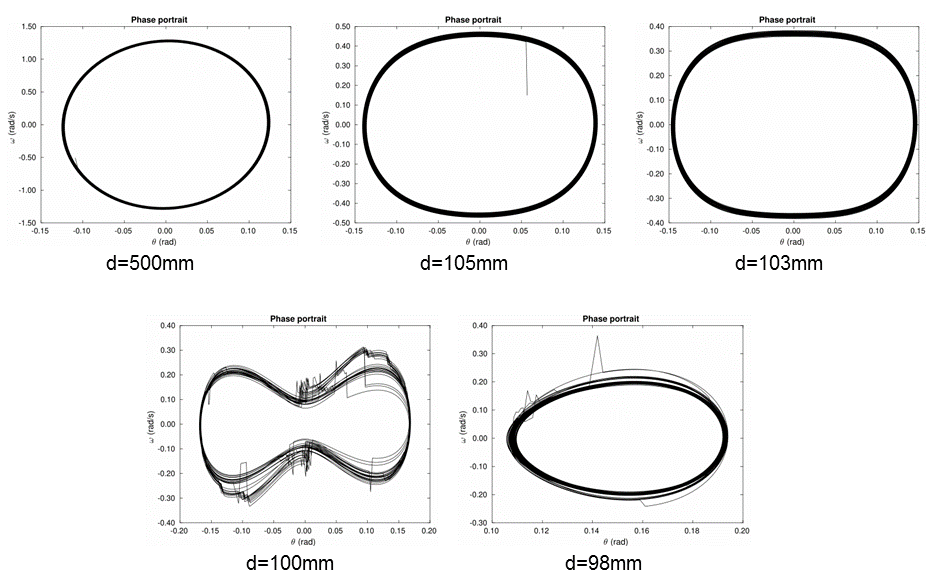
A small change between magnets can lead to sudden and drastic changes in both the qualitative and quantitative nature of the system. For a given value, the behavior is periodic. For another value, it might become aperiodic. This aperiodic system can also exhibit chaos which is ultra-sensitivity to initial conditions.
Generally, chaos begins with period-doubling bifurcation which can be easily seen in the graphs shown below. The system switches from period-1 to period-2 at a precise value of the input parameter, which in our case is the distance d between the two sets of magnets. With further decreases in the value of d, successive bifurcations may take place, which changes the period from twice to four times to finally aperiodic or chaotic. These additional bifurcations are hard to notice but an avid experimenter can always probe deeper.
For this experimental setup, the primary tuning parameter is the distance between two magnets (one at the tip of the pendulum, one on the top of the magnet holder). The horizontal oscillation of the shaft is controlled by the PhysMag Pendulum Software, which is connected to the specially customized Physlogger, which is a part and parcel of this experiment. The time change in angular distance of the pendulum is logged by the same software. The generated data can be displayed in a variety of ways i.e. such as in the form of time series or phase portraits.
Interestingly, we also propose the simulation of the behavior of the magnetic pendulum. This is inbuilt with the accompanying literature. The simulation involves writing an equation of motion that incorporates damping and the magnetic interaction between the magnets. The results are displayed before.
Explore further
- Phase portraits
- Poincare maps
- Bifurcations and Lyapunov exponents
- Hysteresis of nonlinear systems
Major parts included
- Magnetic pendulum machine
- Sets of disk magnets
- Specialized Physlogger with inbuilt motor control
- Qosain Scientific’s analog angle sensor
Not included
- PC
>You can get the PDF version of the brochure by clicking on this link.