Investigating the period, motion, and moment of inertia of the pendulum and its underlying principle.
Description
Pendulums come in various forms and varieties. Here we introduce a swinging rod whose pivot could be changed. Does the time period change and how? Could you build a theoretical model, invoking some basic concepts in mechanics and angular motion? This experiment typifies the exercise of observing a natural phenomenon and finding an underlying principle that explains the observation. In the end, the prediction and outcomes are compared.
Overview
• Mathematical model of a simple swinging rod.
• Investigating period, motion, and moment of inertia.
• Application of the parallel axis theorem.
• Comparing theoretical predictions with experimental observation.
• Calculating uncertainties.
How does it work?
In this experiment, the object of interest is a rectangular wooden rod, specifically, a meter rule of mass M and length L. The rod can be hung on to a pin pivoted on a firm post. To experiment with different moments of inertia, there is a series of holes drilled through the midline of the rod.
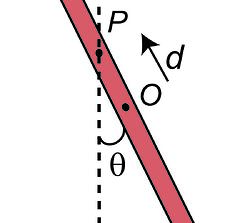
As shown in the figure, the position of the pin is P and the rod is made to swing in a vertical plane about this pivot. The center of mass is, of course, the geometric center of the wooden rod, point O.
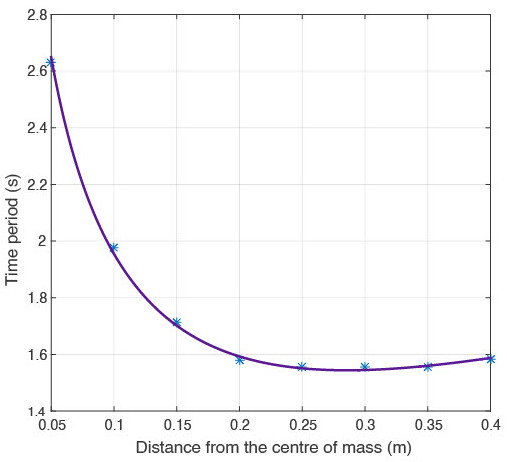
Students are required to measure the time period T of the oscillation with a stopwatch as the pivot P is varied and plot a graph between T and d = OP. These observations are analyzed for uncertainties and compared with the mathematical model.
Parts Included
- Stand
- Rod holder
- Rod
- Stopwatch
You can get the PDF version of the brochure by clicking on this link.